Random Planted Forest
Key Features:
- Maximal order of interaction can be specified. If an order smaller or equal of two is chosen, then the model is directly fully interpretable by plotting the one dimensional functions as curves and the two dimensional functions as heatmaps.
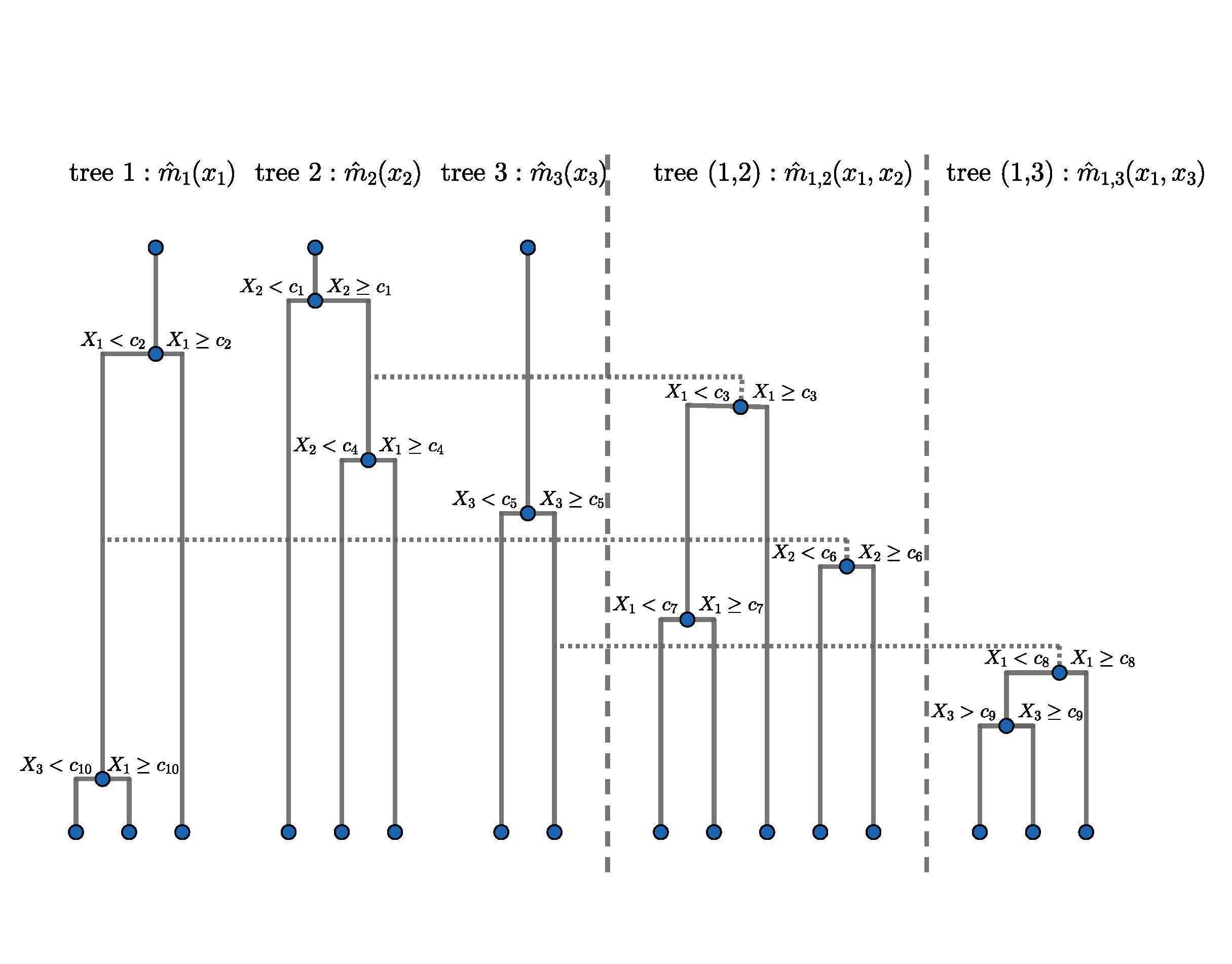
- While fully flexible the algorithm follows a structured path by growing a family of trees simultaneously along a functional ANOVA expansion. Below is an illustration of a family of planted trees. Higher order trees are descendants of lower order trees. Trees grow simultaneously and the height of the edges indicate the order at which splits occurred.
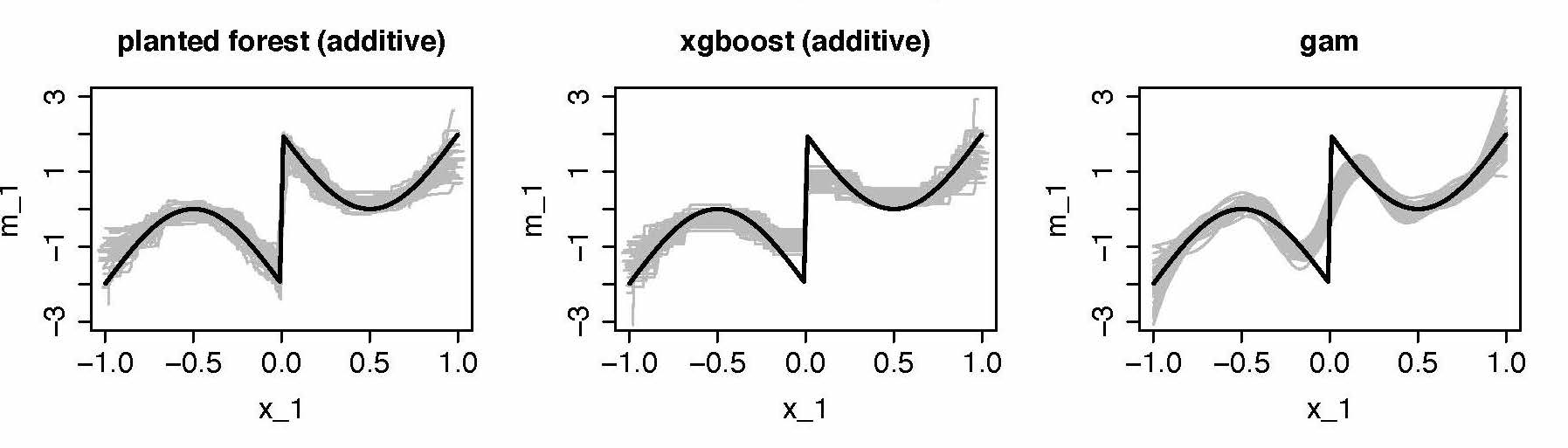
- A first simulation study in our paper shows very promising results. The random planted forest seems able to detect both jumps in the regression function as well as interactions between predictors. In particular in sparse settings, the random planted forest proved an unmatched combination of accuracy and flexibility. Below is an illustration of how the random planted forest shows excellent performance in the detection of jumps.